Literals
Any valid atom is also a valid positive relational literal. The syntax below also allows for negative literals as well as arithmetic expressions as literals. Conjunction may be written with the Unicode character ∧ (U+2227: logical and ).
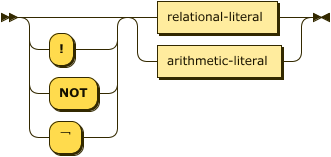
literal ::= ( "!" | "NOT" | "¬" )?
( relational-literal
| arithmetic-literal ) ;

relational-literal
::= atom ;
Examples
The following rules are all equivalent.
ancestor(X, Y) ⟵ parent(X, Z) , ancestor(Z, Y).
ancestor(X, Y) ⟵ parent(X, Z) & ancestor(Z, Y).
ancestor(X, Y) ⟵ parent(X, Z) ∧ ancestor(Z, Y).
ancestor(X, Y) ⟵ parent(X, Z) AND ancestor(Z, Y).
Negation
The language feature negation corresponds to the language $\small\text{Datalog}^{\lnot}$ and
allows the specification of negated literals. Negation may also be written using the Unicode
character ¬ (U+FFE2: full-width not sign). The following rules are equivalent.
.pragma negation.
alive(X) :- person(X), NOT dead(X).
alive(X) ⟵ person(X) ∧ ¬dead(X).
Errors
ERR_NEGATIVE_VARIABLE_NOT_IN_POSITIVE_RELATIONAL_LITERAL– the negated rule is not considered safe.
.pragma negation.
alive(X) :- NOT dead(X).
alive(X) ⟵ ¬dead(X).
Arithmetic Literals
The language feature comparisons corresponds to the language $\small\text{Datalog}^{\theta}$ and
allows the use of arithmetic literals. Comparisons take place between two literals and are
currently limited to a set of common operators. Note the addition of a string match operator, this
is similar to the Perl =~ and requires a string value/variable on the left and a string value or
variable on the right that compiles to a valid Rust regular expression.
Finally, the rule named-term disallows the use of anonymous variables in
arithmetic literals.

arithmetic-literal
::= operand operator operand ;
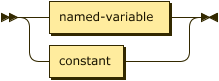
operand ::= ( named-variable | constant ) ;
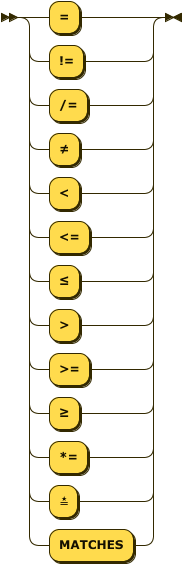
operator
::= "="
| ("!=" | "/=" | "≠")
| "<"
| ("<=" | "≤")
| ">"
| (">=" | "≥")
| ("*=" | "≛" | "MATCHES") ;
The Unicode characters ≠ (not equal to \u{2260}), ≤ (less-than or equal to \u{2264}),
≥ (greater-than or equal to \u{2265}, and star equals \u{e2899b}) may be substituted for the
common arithmetic and string operators.
All arithmetic operations must be between terms of the some type, such that the property compatible introduce above is defined as:
$$\tag{xvi}\small compatible(\tau_{lhs}, \tau_{rhs}, \theta) \leftarrow \tau_{lhs} = \tau_{rhs}$$
Additionally, some operators are not present for all types, as shown in the table below.
| Type | =, ≠ | <, ≤, >, ≥ | ≛ |
|---|---|---|---|
| String | Yes | Yes - lexical | Yes |
| Integer | Yes | Yes | No |
| Decimal | Yes | Yes | No |
| Float | Yes | Yes | No |
| Boolean | Yes | No | No |
Errors
ERR_INCOMPATIBLE_TYPES_FOR_OPERATOR– the two operands have different types; for example1 < true.ERR_INVALID_OPERATOR_FOR_TYPE– the operator is not supported by one, or both, operands22 *= false.
Example
The following is an example using arithmetic literals and the car relation.
.pragma arithmetic_literals.
.assert car(make: string, model: string, age: integer).
antique(X, Y) :- car(X, Y, _) AND X *= "[dD]uesenberg".
antique(X, Y) :- car(X, Y, _) AND Y = "model t".
antique(X, Y) :- car(X, Y, Z) AND Z > 50.